DoWhy: Interpreters for Causal Estimators#

This is a quick introduction to the use of interpreters in the DoWhy causal inference library. We will load in a sample dataset, use different methods for estimating the causal effect of a (pre-specified)treatment variable on a (pre-specified) outcome variable and demonstrate how to interpret the obtained results.

First, let us add the required path for Python to find the DoWhy code and load all required packages

[1]:

%load_ext autoreload
%autoreload 2

[2]:

import numpy as np
import pandas as pd
import logging

import dowhy
from dowhy import CausalModel
import dowhy.datasets

Now, let us load a dataset. For simplicity, we simulate a dataset with linear relationships between common causes and treatment, and common causes and outcome.

Beta is the true causal effect.

[3]:

data = dowhy.datasets.linear_dataset(beta=1,
        num_common_causes=5,
        num_instruments = 2,
        num_treatments=1,
        num_discrete_common_causes=1,
        num_samples=10000,
        treatment_is_binary=True,
        outcome_is_binary=False)
df = data["df"]
print(df[df.v0==True].shape[0])
df

6688

[3]:
Z0 Z1 W0 W1 W2 W3 W4 v0 y
0 0.0 0.360725 -0.658088 -1.242714 -0.904404 -0.374745 0 False -1.605591
1 0.0 0.986901 -1.768959 2.258969 -0.039032 -0.497257 2 True 2.124078
2 0.0 0.209684 0.789630 0.795955 1.021563 0.881734 2 True 3.023497
3 0.0 0.409879 -1.101562 1.423010 -0.026266 -0.711745 1 False 0.450768
4 0.0 0.276523 -0.433493 -0.649299 1.912275 -0.340885 3 False 0.588816
... ... ... ... ... ... ... ... ... ...
9995 0.0 0.553182 -0.533601 -0.399473 -0.209699 -1.442736 2 False -0.851453
9996 0.0 0.813461 -2.522971 2.319158 1.808565 0.430394 0 True 2.740290
9997 0.0 0.695912 -2.093815 0.958733 1.251314 1.271294 2 True 2.475588
9998 0.0 0.566127 -2.189841 2.577861 -0.206154 -0.541626 0 False 0.726954
9999 0.0 0.606514 0.121677 0.972262 0.519804 0.704775 3 True 2.824280

10000 rows × 9 columns

Note that we are using a pandas dataframe to load the data.

Identifying the causal estimand#

We now input a causal graph in the GML graph format.

[4]:

# With graph
model=CausalModel(
        data = df,
        treatment=data["treatment_name"],
        outcome=data["outcome_name"],
        graph=data["gml_graph"],
        instruments=data["instrument_names"]
        )

[5]:

model.view_model()
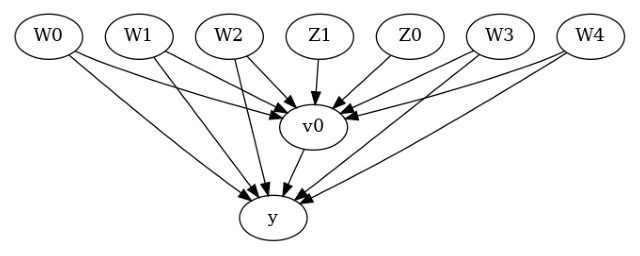
../_images/example_notebooks_dowhy_interpreter_9_0.png 
[6]:

from IPython.display import Image, display
display(Image(filename="causal_model.png"))
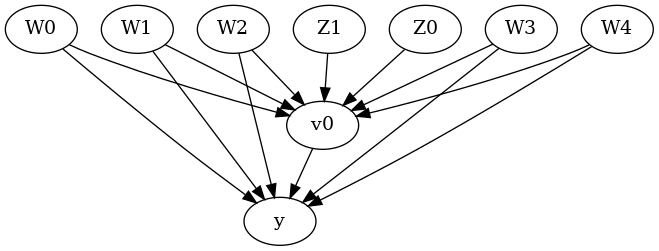
../_images/example_notebooks_dowhy_interpreter_10_0.png

We get a causal graph. Now identification and estimation is done.

[7]:

identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)

Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(E[y|W1,W4,W2,W0,W3])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W2,W0,W3,U) = P(y|v0,W1,W4,W2,W0,W3)

### Estimand : 2
Estimand name: iv
Estimand expression:
 ⎡                              -1⎤
 ⎢    d        ⎛    d          ⎞  ⎥
E⎢─────────(y)⋅⎜─────────([v₀])⎟  ⎥
 ⎣d[Z₁  Z₀]    ⎝d[Z₁  Z₀]      ⎠  ⎦
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)

### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!

Method 1: Propensity Score Stratification#

We will be using propensity scores to stratify units in the data.

[8]:

causal_estimate_strat = model.estimate_effect(identified_estimand,
                                              method_name="backdoor.propensity_score_stratification",
                                              target_units="att")
print(causal_estimate_strat)
print("Causal Estimate is " + str(causal_estimate_strat.value))

*** Causal Estimate ***

## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(E[y|W1,W4,W2,W0,W3])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W2,W0,W3,U) = P(y|v0,W1,W4,W2,W0,W3)

## Realized estimand
b: y~v0+W1+W4+W2+W0+W3
Target units: att

## Estimate
Mean value: 1.0134102267812701

Causal Estimate is 1.0134102267812701

Textual Interpreter#

The textual Interpreter describes (in words) the effect of unit change in the treatment variable on the outcome variable.

[9]:

# Textual Interpreter
interpretation = causal_estimate_strat.interpret(method_name="textual_effect_interpreter")

Increasing the treatment variable(s) [v0] from 0 to 1 causes an increase of 1.0134102267812701 in the expected value of the outcome [['y']], over the data distribution/population represented by the dataset.

Visual Interpreter#

The visual interpreter plots the change in the standardized mean difference (SMD) before and after Propensity Score based adjustment of the dataset. The formula for SMD is given below.

\(SMD = \frac{\bar X_{1} - \bar X_{2}}{\sqrt{(S_{1}^{2} + S_{2}^{2})/2}}\)

Here, \(\bar X_{1}\) and \(\bar X_{2}\) are the sample mean for the treated and control groups.

[10]:

# Visual Interpreter
interpretation = causal_estimate_strat.interpret(method_name="propensity_balance_interpreter")

/home/runner/work/dowhy/dowhy/dowhy/interpreters/propensity_balance_interpreter.py:43: FutureWarning: The provided callable <function mean at 0x7f820057d9d0> is currently using SeriesGroupBy.mean. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "mean" instead.
  mean_diff = df_long.groupby(self.estimate._treatment_name + ["common_cause_id", "strata"]).agg(
/home/runner/work/dowhy/dowhy/dowhy/interpreters/propensity_balance_interpreter.py:57: FutureWarning: The provided callable <function std at 0x7f820057daf0> is currently using SeriesGroupBy.std. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "std" instead.
  stddev_by_w_strata = df_long.groupby(["common_cause_id", "strata"]).agg(stddev=("W", np.std)).reset_index()
/home/runner/work/dowhy/dowhy/dowhy/interpreters/propensity_balance_interpreter.py:63: FutureWarning: The provided callable <function sum at 0x7f8200579a60> is currently using SeriesGroupBy.sum. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "sum" instead.
  mean_diff_strata.groupby("common_cause_id").agg(std_mean_diff=("scaled_mean", np.sum)).reset_index()
/home/runner/work/dowhy/dowhy/dowhy/interpreters/propensity_balance_interpreter.py:67: FutureWarning: The provided callable <function mean at 0x7f820057d9d0> is currently using SeriesGroupBy.mean. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "mean" instead.
  mean_diff_overall = df_long.groupby(self.estimate._treatment_name + ["common_cause_id"]).agg(
/home/runner/work/dowhy/dowhy/dowhy/interpreters/propensity_balance_interpreter.py:74: FutureWarning: The provided callable <function std at 0x7f820057daf0> is currently using SeriesGroupBy.std. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "std" instead.
  stddev_overall = df_long.groupby(["common_cause_id"]).agg(stddev=("W", np.std)).reset_index()
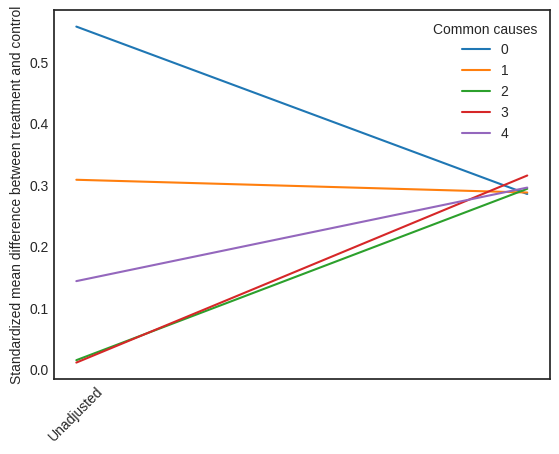
../_images/example_notebooks_dowhy_interpreter_18_1.png

This plot shows how the SMD decreases from the unadjusted to the stratified units.

Method 2: Propensity Score Matching#

We will be using propensity scores to match units in the data.

[11]:

causal_estimate_match = model.estimate_effect(identified_estimand,
                                              method_name="backdoor.propensity_score_matching",
                                              target_units="atc")
print(causal_estimate_match)
print("Causal Estimate is " + str(causal_estimate_match.value))

*** Causal Estimate ***

## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(E[y|W1,W4,W2,W0,W3])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W2,W0,W3,U) = P(y|v0,W1,W4,W2,W0,W3)

## Realized estimand
b: y~v0+W1+W4+W2+W0+W3
Target units: atc

## Estimate
Mean value: 1.0089670448300478

Causal Estimate is 1.0089670448300478

[12]:

# Textual Interpreter
interpretation = causal_estimate_match.interpret(method_name="textual_effect_interpreter")

Increasing the treatment variable(s) [v0] from 0 to 1 causes an increase of 1.0089670448300478 in the expected value of the outcome [['y']], over the data distribution/population represented by the dataset.

Cannot use propensity balance interpretor here since the interpreter method only supports propensity score stratification estimator.

Method 3: Weighting#

We will be using (inverse) propensity scores to assign weights to units in the data. DoWhy supports a few different weighting schemes:

  1. Vanilla Inverse Propensity Score weighting (IPS) (weighting_scheme=”ips_weight”)

  2. Self-normalized IPS weighting (also known as the Hajek estimator) (weighting_scheme=”ips_normalized_weight”)

  3. Stabilized IPS weighting (weighting_scheme = “ips_stabilized_weight”)

[13]:

causal_estimate_ipw = model.estimate_effect(identified_estimand,
                                            method_name="backdoor.propensity_score_weighting",
                                            target_units = "ate",
                                            method_params={"weighting_scheme":"ips_weight"})
print(causal_estimate_ipw)
print("Causal Estimate is " + str(causal_estimate_ipw.value))

*** Causal Estimate ***

## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(E[y|W1,W4,W2,W0,W3])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W2,W0,W3,U) = P(y|v0,W1,W4,W2,W0,W3)

## Realized estimand
b: y~v0+W1+W4+W2+W0+W3
Target units: ate

## Estimate
Mean value: 1.0096820011588112

Causal Estimate is 1.0096820011588112

[14]:

# Textual Interpreter
interpretation = causal_estimate_ipw.interpret(method_name="textual_effect_interpreter")

Increasing the treatment variable(s) [v0] from 0 to 1 causes an increase of 1.0096820011588112 in the expected value of the outcome [['y']], over the data distribution/population represented by the dataset.

[15]:

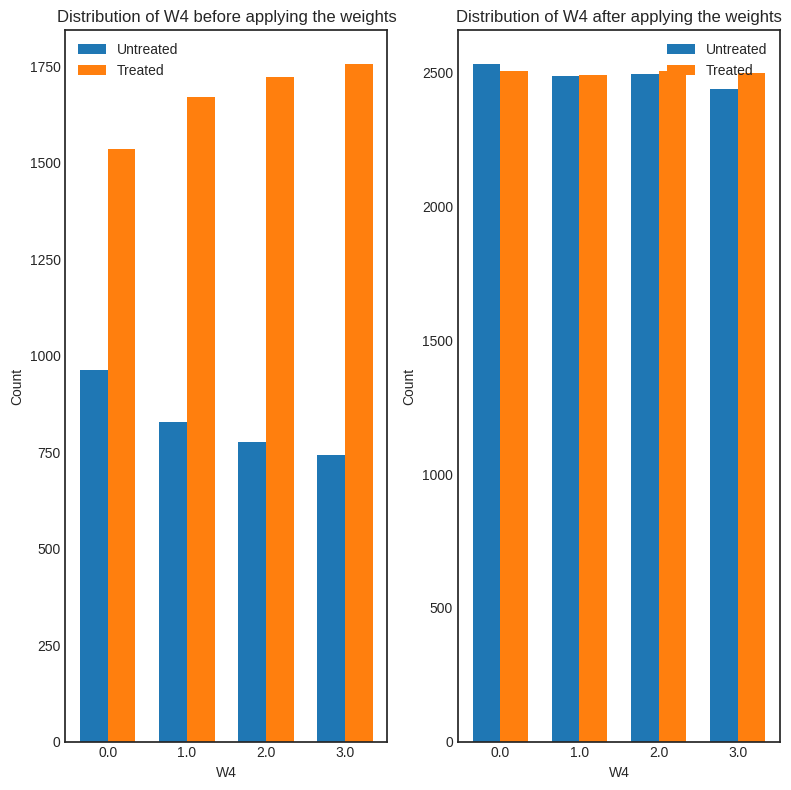
interpretation = causal_estimate_ipw.interpret(method_name="confounder_distribution_interpreter", fig_size=(8,8), font_size=12, var_name='W4', var_type='discrete')

/home/runner/work/dowhy/dowhy/dowhy/interpreters/confounder_distribution_interpreter.py:83: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  barplot_df_before = df.groupby([self.var_name, treated]).size().reset_index(name="count")
/home/runner/work/dowhy/dowhy/dowhy/interpreters/confounder_distribution_interpreter.py:86: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  barplot_df_after = df.groupby([self.var_name, treated]).agg({"weight": np.sum}).reset_index()
/home/runner/work/dowhy/dowhy/dowhy/interpreters/confounder_distribution_interpreter.py:86: FutureWarning: The provided callable <function sum at 0x7f8200579a60> is currently using SeriesGroupBy.sum. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "sum" instead.
  barplot_df_after = df.groupby([self.var_name, treated]).agg({"weight": np.sum}).reset_index()
../_images/example_notebooks_dowhy_interpreter_27_1.png 
[ ]: