Demo for the DoWhy causal API

We show a simple example of adding a causal extension to any dataframe.

import dowhy.datasets
import dowhy.api
from dowhy.graph import build_graph_from_str

import numpy as np
import pandas as pd

from statsmodels.api import OLS

data = dowhy.datasets.linear_dataset(beta=5,
        num_common_causes=1,
        num_instruments = 0,
        num_samples=1000,
        treatment_is_binary=True)
df = data['df']
df['y'] = df['y'] + np.random.normal(size=len(df)) # Adding noise to data. Without noise, the variance in Y|X, Z is zero, and mcmc fails.
nx_graph = build_graph_from_str(data["dot_graph"])

treatment= data["treatment_name"][0]
outcome = data["outcome_name"][0]
common_cause = data["common_causes_names"][0]
df

	W0	v0	y
0	1.524459	False	2.894592
1	0.597564	True	5.522022
2	-0.918363	False	-1.742012
3	-0.144220	False	-0.553316
4	0.277026	True	6.652711
...	...	...	...
995	0.275157	False	-0.155439
996	-0.490586	True	2.751520
997	0.386001	False	1.374444
998	0.623935	True	6.125341
999	-0.750355	False	-1.535576

1000 rows × 3 columns

# data['df'] is just a regular pandas.DataFrame
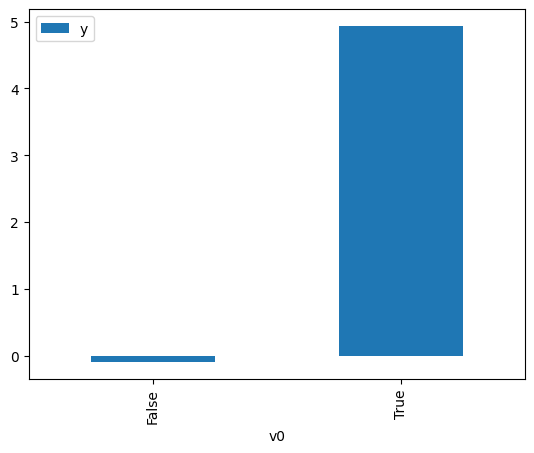
df.causal.do(x=treatment,
             variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
             outcome=outcome,
             common_causes=[common_cause],
            ).groupby(treatment).mean().plot(y=outcome, kind='bar')

<Axes: xlabel='v0'>

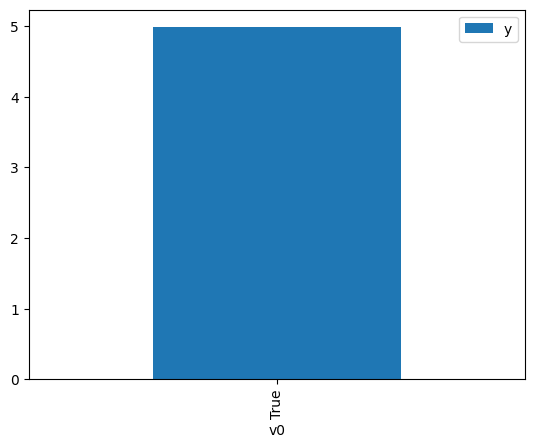
df.causal.do(x={treatment: 1},
              variable_types={treatment:'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              method='weighting',
              common_causes=[common_cause]
              ).groupby(treatment).mean().plot(y=outcome, kind='bar')

<Axes: xlabel='v0'>

cdf_1 = df.causal.do(x={treatment: 1},
              variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              graph=nx_graph
              )

cdf_0 = df.causal.do(x={treatment: 0},
              variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              graph=nx_graph
              )

cdf_0

	W0	v0	y	propensity_score	weight
0	0.686850	False	1.336979	0.307573	3.251263
1	-0.968684	False	-2.292953	0.719606	1.389649
2	0.208372	False	1.270343	0.424444	2.356022
3	-0.039039	False	0.876932	0.489394	2.043342
4	1.195703	False	1.539124	0.205771	4.859778
...	...	...	...	...	...
995	1.606665	False	2.004791	0.143562	6.965625
996	1.336141	False	2.721816	0.182515	5.479001
997	-0.143527	False	-0.421825	0.517062	1.934005
998	-0.399153	False	-1.246800	0.583973	1.712409
999	-1.832077	False	-2.103029	0.864976	1.156101

1000 rows × 5 columns

cdf_1

	W0	v0	y	propensity_score	weight
0	0.486018	True	5.731617	0.645362	1.549517
1	-2.019900	True	1.438117	0.113423	8.816575
2	0.779625	True	5.351522	0.712956	1.402611
3	1.599964	True	9.187401	0.855563	1.168821
4	-1.085253	True	3.149118	0.256163	3.903769
...	...	...	...	...	...
995	1.028011	True	6.188327	0.763677	1.309455
996	-0.070812	True	6.911912	0.502191	1.991272
997	-1.238410	True	1.942119	0.226483	4.415339
998	0.120633	True	6.926872	0.552703	1.809290
999	-1.844860	True	2.818377	0.133450	7.493462

1000 rows × 5 columns

Comparing the estimate to Linear Regression

First, estimating the effect using the causal data frame, and the 95% confidence interval.

(cdf_1['y'] - cdf_0['y']).mean()

$\displaystyle 4.81384155047008$

1.96*(cdf_1['y'] - cdf_0['y']).std() / np.sqrt(len(df))

$\displaystyle 0.160219938187493$

Comparing to the estimate from OLS.

model = OLS(np.asarray(df[outcome]), np.asarray(df[[common_cause, treatment]], dtype=np.float64))
result = model.fit()
result.summary()

OLS Regression Results

Dep. Variable:	y	R-squared (uncentered):	0.955
Model:	OLS	Adj. R-squared (uncentered):	0.954
Method:	Least Squares	F-statistic:	1.047e+04
Date:	Tue, 26 Aug 2025	Prob (F-statistic):	0.00
Time:	20:27:55	Log-Likelihood:	-1375.7
No. Observations:	1000	AIC:	2755.
Df Residuals:	998	BIC:	2765.
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
x1	1.5378	0.031	48.913	0.000	1.476	1.600
x2	5.0199	0.044	113.339	0.000	4.933	5.107

Omnibus:	3.734	Durbin-Watson:	1.931
Prob(Omnibus):	0.155	Jarque-Bera (JB):	3.814
Skew:	-0.092	Prob(JB):	0.149
Kurtosis:	3.240	Cond. No.	1.62

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.