DoWhy: Different estimation methods for causal inference

This is a quick introduction to the DoWhy causal inference library. We will load in a sample dataset and use different methods for estimating the causal effect of a (pre-specified)treatment variable on a (pre-specified) outcome variable.

We will see that not all estimators return the correct effect for this dataset.

First, let us add the required path for Python to find the DoWhy code and load all required packages

[1]:

import os, sys
sys.path.append(os.path.abspath("../../../"))

[2]:

import numpy as np
import pandas as pd
import logging

import dowhy
from dowhy import CausalModel
import dowhy.datasets

Now, let us load a dataset. For simplicity, we simulate a dataset with linear relationships between common causes and treatment, and common causes and outcome.

Beta is the true causal effect.

[3]:

data = dowhy.datasets.linear_dataset(beta=10,
        num_common_causes=5,
        num_instruments = 2,
        num_treatments=1,
        num_samples=10000,
        treatment_is_binary=True,
        outcome_is_binary=False)
df = data["df"]
df

[3]:

	Z0	Z1	W0	W1	W2	W3	W4	v0	y
0	1.0	0.691789	2.048005	1.201252	1.137812	0.717649	0.352527	True	27.023672
1	0.0	0.928185	-0.660520	0.407551	1.025260	1.997749	-2.104250	True	9.889046
2	0.0	0.833675	-0.905044	-0.130040	0.565832	0.653425	1.568407	True	14.894928
3	0.0	0.612402	0.158018	-1.123704	1.675350	0.826259	-0.888828	True	8.971762
4	0.0	0.785270	0.726382	-1.202901	-1.058051	2.205015	0.495726	True	20.896262
...	...	...	...	...	...	...	...	...	...
9995	0.0	0.894599	-0.712648	-0.050668	1.503133	-0.027247	0.381114	True	9.005796
9996	0.0	0.025013	-0.670075	-0.248390	-0.085291	-0.024445	1.337857	True	11.338158
9997	0.0	0.428422	-0.461601	-0.255573	-0.642571	-1.268839	0.112462	False	-8.186703
9998	1.0	0.041934	0.627985	-1.740130	1.426222	2.741662	0.558544	True	23.082221
9999	0.0	0.355128	0.414349	0.956478	0.567128	0.305772	0.808131	True	19.008151

10000 rows × 9 columns

Note that we are using a pandas dataframe to load the data.

Identifying the causal estimand

We now input a causal graph in the DOT graph format.

[4]:

# With graph
model=CausalModel(
        data = df,
        treatment=data["treatment_name"],
        outcome=data["outcome_name"],
        graph=data["gml_graph"],
        instruments=data["instrument_names"],
        logging_level = logging.INFO
        )

INFO:dowhy.causal_model:Model to find the causal effect of treatment ['v0'] on outcome ['y']

[5]:

model.view_model()

[6]:

from IPython.display import Image, display
display(Image(filename="causal_model.png"))

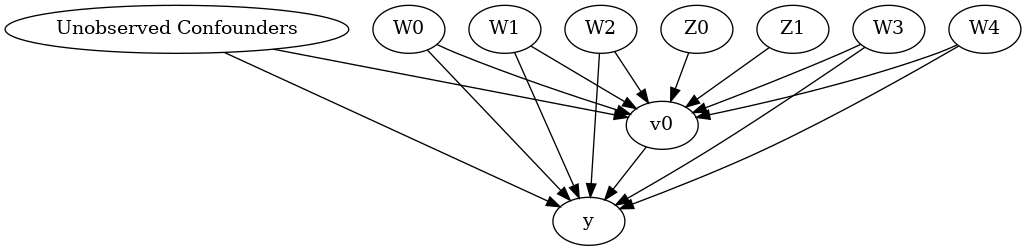
../_images/example_notebooks_dowhy_estimation_methods_10_0.png

We get a causal graph. Now identification and estimation is done.

[7]:

identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)

WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:['Z1', 'Z0']
INFO:dowhy.causal_identifier:Frontdoor variables for treatment and outcome:[]

Estimand type: nonparametric-ate

### Estimand : 1
Estimand name: backdoor1 (Default)
Estimand expression:
  d
─────(Expectation(y|W3,W4,W1,W2,W0))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W3,W4,W1,W2,W0,U) = P(y|v0,W3,W4,W1,W2,W0)

### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z1, Z0])*Derivative([v0], [Z1, Z0])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)

### Estimand : 3
Estimand name: frontdoor
No such variable found!

Method 1: Regression

Use linear regression.

[8]:

causal_estimate_reg = model.estimate_effect(identified_estimand,
        method_name="backdoor.linear_regression",
        test_significance=True)
print(causal_estimate_reg)
print("Causal Estimate is " + str(causal_estimate_reg.value))

INFO:dowhy.causal_estimator:b: y~v0+W3+W4+W1+W2+W0
INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator

*** Causal Estimate ***

## Identified estimand
Estimand type: nonparametric-ate

## Realized estimand
b: y~v0+W3+W4+W1+W2+W0
Target units: ate

## Estimate
Mean value: 9.999820423120656
p-value: [0.]

Causal Estimate is 9.999820423120656

Method 2: Stratification

We will be using propensity scores to stratify units in the data.

[9]:

causal_estimate_strat = model.estimate_effect(identified_estimand,
                                              method_name="backdoor.propensity_score_stratification",
                                              target_units="att")
print(causal_estimate_strat)
print("Causal Estimate is " + str(causal_estimate_strat.value))

INFO:dowhy.causal_estimator:INFO: Using Propensity Score Stratification Estimator
INFO:dowhy.causal_estimator:b: y~v0+W3+W4+W1+W2+W0
/home/amit/py-envs/env3.8/lib/python3.8/site-packages/sklearn/utils/validation.py:72: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  return f(**kwargs)

*** Causal Estimate ***

## Identified estimand
Estimand type: nonparametric-ate

## Realized estimand
b: y~v0+W3+W4+W1+W2+W0
Target units: att

## Estimate
Mean value: 9.990307279763607

Causal Estimate is 9.990307279763607

Method 3: Matching

We will be using propensity scores to match units in the data.

[10]:

causal_estimate_match = model.estimate_effect(identified_estimand,
                                              method_name="backdoor.propensity_score_matching",
                                              target_units="atc")
print(causal_estimate_match)
print("Causal Estimate is " + str(causal_estimate_match.value))

INFO:dowhy.causal_estimator:INFO: Using Propensity Score Matching Estimator
INFO:dowhy.causal_estimator:b: y~v0+W3+W4+W1+W2+W0
/home/amit/py-envs/env3.8/lib/python3.8/site-packages/sklearn/utils/validation.py:72: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  return f(**kwargs)

*** Causal Estimate ***

## Identified estimand
Estimand type: nonparametric-ate

## Realized estimand
b: y~v0+W3+W4+W1+W2+W0
Target units: atc

## Estimate
Mean value: 10.158795156282878

Causal Estimate is 10.158795156282878

Method 4: Weighting

We will be using (inverse) propensity scores to assign weights to units in the data. DoWhy supports a few different weighting schemes: 1. Vanilla Inverse Propensity Score weighting (IPS) (weighting_scheme=“ips_weight”) 2. Self-normalized IPS weighting (also known as the Hajek estimator) (weighting_scheme=“ips_normalized_weight”) 3. Stabilized IPS weighting (weighting_scheme = “ips_stabilized_weight”)

[11]:

causal_estimate_ipw = model.estimate_effect(identified_estimand,
                                            method_name="backdoor.propensity_score_weighting",
                                            target_units = "ate",
                                            method_params={"weighting_scheme":"ips_weight"})
print(causal_estimate_ipw)
print("Causal Estimate is " + str(causal_estimate_ipw.value))

INFO:dowhy.causal_estimator:INFO: Using Propensity Score Weighting Estimator
INFO:dowhy.causal_estimator:b: y~v0+W3+W4+W1+W2+W0

*** Causal Estimate ***

## Identified estimand
Estimand type: nonparametric-ate

## Realized estimand
b: y~v0+W3+W4+W1+W2+W0
Target units: ate

## Estimate
Mean value: 13.708275713548172

Causal Estimate is 13.708275713548172

/home/amit/py-envs/env3.8/lib/python3.8/site-packages/sklearn/utils/validation.py:72: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  return f(**kwargs)

Method 5: Instrumental Variable

We will be using the Wald estimator for the provided instrumental variable.

[12]:

causal_estimate_iv = model.estimate_effect(identified_estimand,
        method_name="iv.instrumental_variable", method_params = {'iv_instrument_name': 'Z0'})
print(causal_estimate_iv)
print("Causal Estimate is " + str(causal_estimate_iv.value))

INFO:dowhy.causal_estimator:INFO: Using Instrumental Variable Estimator
INFO:dowhy.causal_estimator:Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:
                                                              -1
Expectation(Derivative(y, Z0))⋅Expectation(Derivative(v0, Z0))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['v0'] is affected in the same way by common causes of ['v0'] and y
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome y is affected in the same way by common causes of ['v0'] and y

*** Causal Estimate ***

## Identified estimand
Estimand type: nonparametric-ate

### Estimand : 1
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z1, Z0])*Derivative([v0], [Z1, Z0])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)

## Realized estimand
Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:
                                                              -1
Expectation(Derivative(y, Z0))⋅Expectation(Derivative(v0, Z0))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['v0'] is affected in the same way by common causes of ['v0'] and y
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome y is affected in the same way by common causes of ['v0'] and y

Target units: ate

## Estimate
Mean value: 10.976391486033847

Causal Estimate is 10.976391486033847

Method 6: Regression Discontinuity

We will be internally converting this to an equivalent instrumental variables problem.

[13]:

causal_estimate_regdist = model.estimate_effect(identified_estimand,
        method_name="iv.regression_discontinuity",
        method_params={'rd_variable_name':'Z1',
                       'rd_threshold_value':0.5,
                       'rd_bandwidth': 0.1})
print(causal_estimate_regdist)
print("Causal Estimate is " + str(causal_estimate_regdist.value))

INFO:dowhy.causal_estimator:Using Regression Discontinuity Estimator
INFO:dowhy.causal_estimator:
INFO:dowhy.causal_estimator:INFO: Using Instrumental Variable Estimator
INFO:dowhy.causal_estimator:Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:

Expectation(Derivative(y, local_rd_variable))⋅Expectation(Derivative(v0, local

              -1
_rd_variable))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['local_treatment'] is affected in the same way by common causes of ['local_treatment'] and local_outcome
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome local_outcome is affected in the same way by common causes of ['local_treatment'] and local_outcome

      local_rd_variable  local_treatment  local_outcome
5              0.410031             True       8.181771
11             0.464060             True      13.104927
23             0.589359             True      -1.627049
29             0.508903             True      26.879421
30             0.591489             True      18.278407
...                 ...              ...            ...
9940           0.465609             True      19.298413
9941           0.420378             True       9.461016
9945           0.571843             True       0.752238
9968           0.545650             True       7.979716
9997           0.428422            False      -8.186703

[1966 rows x 3 columns]
*** Causal Estimate ***

## Identified estimand
Estimand type: nonparametric-ate

### Estimand : 1
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z1, Z0])*Derivative([v0], [Z1, Z0])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)

## Realized estimand
Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:

Expectation(Derivative(y, local_rd_variable))⋅Expectation(Derivative(v0, local

              -1
_rd_variable))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['local_treatment'] is affected in the same way by common causes of ['local_treatment'] and local_outcome
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome local_outcome is affected in the same way by common causes of ['local_treatment'] and local_outcome

Target units: ate

## Estimate
Mean value: -7.883709534515737

Causal Estimate is -7.883709534515737