DoWhy: Different estimation methods for causal inference
This is a quick introduction to the DoWhy causal inference library. We will load in a sample dataset and use different methods for estimating the causal effect of a (pre-specified)treatment variable on a (pre-specified) outcome variable.
We will see that not all estimators return the correct effect for this dataset.
First, let us add the required path for Python to find the DoWhy code and load all required packages
[1]:
import numpy as np
import pandas as pd
import logging
import dowhy
from dowhy import CausalModel
import dowhy.datasets
Now, let us load a dataset. For simplicity, we simulate a dataset with linear relationships between common causes and treatment, and common causes and outcome.
Beta is the true causal effect.
[2]:
data = dowhy.datasets.linear_dataset(beta=10,
num_common_causes=5,
num_instruments = 2,
num_treatments=1,
num_samples=10000,
treatment_is_binary=True,
outcome_is_binary=False)
df = data["df"]
df
[2]:
| Z0 | Z1 | W0 | W1 | W2 | W3 | W4 | v0 | y | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0.521013 | -1.325391 | 2.116213 | -0.557359 | -1.865444 | 1.605934 | False | 10.352212 |
| 1 | 0.0 | 0.463769 | 1.069812 | 1.726722 | -0.610115 | 0.350867 | 0.882315 | True | 19.499769 |
| 2 | 0.0 | 0.125765 | -1.945924 | 1.484627 | -1.575032 | 0.520069 | 0.559467 | False | 2.205429 |
| 3 | 0.0 | 0.861999 | -0.221328 | 0.939332 | 0.065349 | 1.291141 | 0.056167 | True | 12.968877 |
| 4 | 0.0 | 0.893044 | -0.533583 | 2.024348 | -0.227786 | -2.962155 | 0.057679 | True | 14.847690 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 9995 | 0.0 | 0.019696 | -0.518280 | 2.516658 | -3.063094 | -1.035060 | 1.231945 | False | 7.816809 |
| 9996 | 0.0 | 0.692714 | -0.510823 | 0.612004 | -0.758462 | -1.786669 | 1.217035 | True | 15.047879 |
| 9997 | 0.0 | 0.164993 | 0.190624 | 0.365532 | -0.312707 | 0.794803 | 2.458445 | True | 21.472658 |
| 9998 | 0.0 | 0.382386 | -2.654195 | 1.469548 | -2.191149 | -0.681429 | 1.197488 | False | 2.936543 |
| 9999 | 0.0 | 0.713687 | -0.799016 | 0.810676 | -0.969194 | -0.467067 | 1.327113 | True | 15.621830 |
10000 rows × 9 columns
Note that we are using a pandas dataframe to load the data.
Identifying the causal estimand
We now input a causal graph in the DOT graph format.
[3]:
# With graph
model=CausalModel(
data = df,
treatment=data["treatment_name"],
outcome=data["outcome_name"],
graph=data["gml_graph"],
instruments=data["instrument_names"]
)
[4]:
model.view_model()
[5]:
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
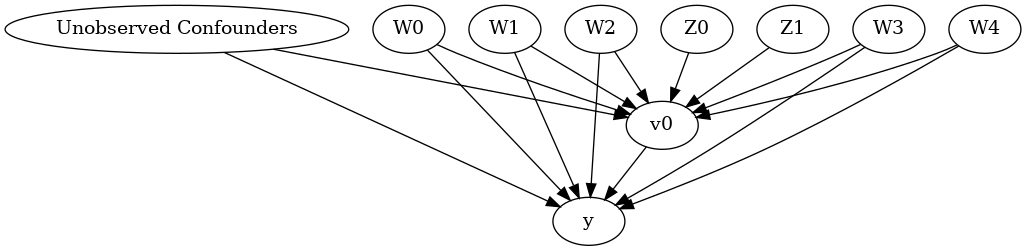
We get a causal graph. Now identification and estimation is done.
[6]:
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(Expectation(y|W0,W1,W3,W4,W2))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,W3,W4,W2,U) = P(y|v0,W0,W1,W3,W4,W2)
### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
### Estimand : 3
Estimand name: frontdoor
No such variable found!
Method 1: Regression
Use linear regression.
[7]:
causal_estimate_reg = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression",
test_significance=True)
print(causal_estimate_reg)
print("Causal Estimate is " + str(causal_estimate_reg.value))
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(Expectation(y|W0,W1,W3,W4,W2))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,W3,W4,W2,U) = P(y|v0,W0,W1,W3,W4,W2)
## Realized estimand
b: y~v0+W0+W1+W3+W4+W2
Target units: ate
## Estimate
Mean value: 10.00020571565491
p-value: [0.]
Causal Estimate is 10.00020571565491
Method 2: Stratification
We will be using propensity scores to stratify units in the data.
[8]:
causal_estimate_strat = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_stratification",
target_units="att")
print(causal_estimate_strat)
print("Causal Estimate is " + str(causal_estimate_strat.value))
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(Expectation(y|W0,W1,W3,W4,W2))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,W3,W4,W2,U) = P(y|v0,W0,W1,W3,W4,W2)
## Realized estimand
b: y~v0+W0+W1+W3+W4+W2
Target units: att
## Estimate
Mean value: 10.019860140019505
Causal Estimate is 10.019860140019505
/home/amit/py-envs/env3.8/lib/python3.8/site-packages/sklearn/utils/validation.py:72: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
return f(**kwargs)
Method 3: Matching
We will be using propensity scores to match units in the data.
[9]:
causal_estimate_match = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_matching",
target_units="atc")
print(causal_estimate_match)
print("Causal Estimate is " + str(causal_estimate_match.value))
/home/amit/py-envs/env3.8/lib/python3.8/site-packages/sklearn/utils/validation.py:72: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
return f(**kwargs)
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(Expectation(y|W0,W1,W3,W4,W2))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,W3,W4,W2,U) = P(y|v0,W0,W1,W3,W4,W2)
## Realized estimand
b: y~v0+W0+W1+W3+W4+W2
Target units: atc
## Estimate
Mean value: 9.752837406069007
Causal Estimate is 9.752837406069007
Method 4: Weighting
We will be using (inverse) propensity scores to assign weights to units in the data. DoWhy supports a few different weighting schemes: 1. Vanilla Inverse Propensity Score weighting (IPS) (weighting_scheme=“ips_weight”) 2. Self-normalized IPS weighting (also known as the Hajek estimator) (weighting_scheme=“ips_normalized_weight”) 3. Stabilized IPS weighting (weighting_scheme = “ips_stabilized_weight”)
[10]:
causal_estimate_ipw = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_weighting",
target_units = "ate",
method_params={"weighting_scheme":"ips_weight"})
print(causal_estimate_ipw)
print("Causal Estimate is " + str(causal_estimate_ipw.value))
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(Expectation(y|W0,W1,W3,W4,W2))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,W3,W4,W2,U) = P(y|v0,W0,W1,W3,W4,W2)
## Realized estimand
b: y~v0+W0+W1+W3+W4+W2
Target units: ate
## Estimate
Mean value: 12.690127182579836
Causal Estimate is 12.690127182579836
/home/amit/py-envs/env3.8/lib/python3.8/site-packages/sklearn/utils/validation.py:72: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
return f(**kwargs)
Method 5: Instrumental Variable
We will be using the Wald estimator for the provided instrumental variable.
[11]:
causal_estimate_iv = model.estimate_effect(identified_estimand,
method_name="iv.instrumental_variable", method_params = {'iv_instrument_name': 'Z0'})
print(causal_estimate_iv)
print("Causal Estimate is " + str(causal_estimate_iv.value))
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
## Realized estimand
Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:
-1
Expectation(Derivative(y, Z0))⋅Expectation(Derivative(v0, Z0))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['v0'] is affected in the same way by common causes of ['v0'] and y
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome y is affected in the same way by common causes of ['v0'] and y
Target units: ate
## Estimate
Mean value: 11.085627630661348
Causal Estimate is 11.085627630661348
Method 6: Regression Discontinuity
We will be internally converting this to an equivalent instrumental variables problem.
[12]:
causal_estimate_regdist = model.estimate_effect(identified_estimand,
method_name="iv.regression_discontinuity",
method_params={'rd_variable_name':'Z1',
'rd_threshold_value':0.5,
'rd_bandwidth': 0.1})
print(causal_estimate_regdist)
print("Causal Estimate is " + str(causal_estimate_regdist.value))
local_rd_variable local_treatment local_outcome
0 0.521013 False 10.352212
1 0.463769 True 19.499769
9 0.477009 True 15.650173
13 0.500243 False -0.607821
16 0.596191 True 7.387162
... ... ... ...
9980 0.449123 False 15.319816
9982 0.501416 True 15.874824
9983 0.447196 True 8.519615
9985 0.499184 False -0.135301
9990 0.475909 True 19.444943
[2005 rows x 3 columns]
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
## Realized estimand
Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:
Expectation(Derivative(y, local_rd_variable))⋅Expectation(Derivative(v0, local
-1
_rd_variable))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['local_treatment'] is affected in the same way by common causes of ['local_treatment'] and local_outcome
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome local_outcome is affected in the same way by common causes of ['local_treatment'] and local_outcome
Target units: ate
## Estimate
Mean value: 17.24115839926478
Causal Estimate is 17.24115839926478