Using prior knowledge in order-based algorithms for causal discovery

We illustrate how to exploit prior knowledge and assumptions about the causal structure that generates the data in the context of causal discovery with order-based algorithms.

import numpy as np
import networkx as nx
from scipy import stats
import pandas as pd
from pywhy_graphs.viz import draw
from dodiscover import make_context
from dodiscover.toporder.score import SCORE
from dowhy import gcm
from dowhy.gcm.util.general import set_random_seed

Simulate some data

First we will simulate data, starting from an Additive Noise Model (ANM). This will then induce a causal graph, which we can visualize.

# set a random seed to make example reproducible
seed = 12345
rng = np.random.RandomState(seed=seed)


class MyCustomModel(gcm.PredictionModel):
    def __init__(self, coefficient):
        self.coefficient = coefficient

    def fit(self, X, Y):
        # Nothing to fit here, since we know the ground truth.
        pass

    def predict(self, X):
        return self.coefficient * X

    def clone(self):
        # We don't really need this actually.
        return MyCustomModel(self.coefficient)


# set a random seed to make example reproducible
set_random_seed(1234)

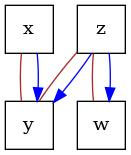
# construct a causal graph that will result in
# x -> y <- z -> w
G = nx.DiGraph([("x", "y"), ("z", "y"), ("z", "w")])

causal_model = gcm.ProbabilisticCausalModel(G)
causal_model.set_causal_mechanism("x", gcm.ScipyDistribution(stats.binom, p=0.5, n=1))
causal_model.set_causal_mechanism("z", gcm.ScipyDistribution(stats.binom, p=0.9, n=1))
causal_model.set_causal_mechanism(
    "y",
    gcm.AdditiveNoiseModel(
        prediction_model=MyCustomModel(1),
        noise_model=gcm.ScipyDistribution(stats.binom, p=0.8, n=1),
    ),
)
causal_model.set_causal_mechanism(
    "w",
    gcm.AdditiveNoiseModel(
        prediction_model=MyCustomModel(1),
        noise_model=gcm.ScipyDistribution(stats.binom, p=0.5, n=1),
    ),
)

# Fit here would not really fit parameters, since we don't do anything in the fit method.
# Here, we only need this to ensure that each FCM has the correct local hash (i.e., we
# get an inconsistency error if we would modify the graph afterwards without updating
# the FCMs). Having an empty data set is a small workaround, since all models are
# pre-defined.
gcm.fit(causal_model, pd.DataFrame(columns=["x", "y", "z", "w"]))

# sample the observational data
data = gcm.draw_samples(causal_model, num_samples=500)

print(data.head())
print(pd.Series({col: data[col].unique() for col in data}))
dot_graph = draw(G)
dot_graph.render(outfile="oracle_dag.png", view=True)

Fitting causal models:   0%|          | 0/4 [00:00<?, ?it/s]
Fitting causal mechanism of node x:   0%|          | 0/4 [00:00<?, ?it/s]
Fitting causal mechanism of node y:   0%|          | 0/4 [00:00<?, ?it/s]
Fitting causal mechanism of node z:   0%|          | 0/4 [00:00<?, ?it/s]
Fitting causal mechanism of node w:   0%|          | 0/4 [00:00<?, ?it/s]
Fitting causal mechanism of node w: 100%|##########| 4/4 [00:00<00:00, 1880.22it/s]
   x  ...  w
0  0  ...  1
1  1  ...  2
2  0  ...  1
3  1  ...  1
4  1  ...  1

[5 rows x 4 columns]
x       [0, 1]
z       [1, 0]
y    [1, 2, 0]
w    [1, 2, 0]
dtype: object

'oracle_dag.png'

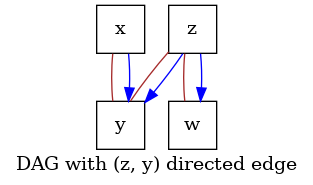
Define the context with fixed edges

Define the context specifying the fixed directed edge (z, y) in the output graph. This encodes prior domain information from the user, which specifies that there is a directed connection between z and y.

included_edges = nx.DiGraph([("z", "y")])
context = make_context().variables(data=data).edges(include=included_edges).build()

Run structure learning algorithm with fixed edges

Now we run inference with the SCORE algorithm. The output of the inference must be a graph including (z, y) in the set of edges.

score = SCORE()  # or DAS() or NoGAM() or CAM()
score.learn_graph(data, context)

# Verify that the output includes (`z`, `y`) in the set of edges.
graph = score.graph_
dot_graph = draw(graph, name="DAG with (z, y) directed edge")
dot_graph.render(outfile="score_prior_include.png", view=True)

'score_prior_include.png'

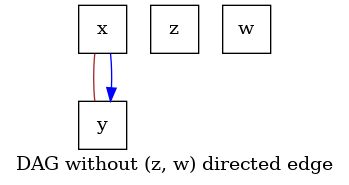
Define the context with excluded edges

The context can also be used to encode prior information about directed edges that must be excluded from the the output graph. In this example, we define the context that excludes the edge (z, w) from the output DAG.

excluded_edges = nx.DiGraph([("z", "w")])
context = make_context().variables(data=data).edges(exclude=excluded_edges).build()

# Run structure learning algorithm with excluded edges
# ----------------------------------------------------
# Now we run inference with the SCORE algorithm. The edge (`z`, `w`)
# must not appear in the output graph.
score = SCORE()  # or DAS() or NoGAM() or CAM()
score.learn_graph(data, context)

# Verify that the output does not include (`z`, `w`) in the set of edges.
graph = score.graph_
dot_graph = draw(graph, name="DAG without (z, w) directed edge")
dot_graph.render(outfile="score_prior_exclude.png", view=True)

'score_prior_exclude.png'

Summary

In this tutorial we show how to encode prior knowledge about the solution with the context object, in the setting of causal discovery with order-based algorithms. This example can be generalized to the case of NoGAM, DAS, and CAM methods. For a detailed example on order-based discovery approaches, see this tutorial.